Explain arithmetic encoding process with an example.
Arithmetic coding:
Unlike the variable-length codes described previously, arithmetic coding generates nonblock codes. In arithmetic coding, which can be traced to the work of Elias, a one-to-one correspondence between source symbols and code words does not exist. Instead, an entire sequence of source symbols (or message) is assigned a single arithmetic code word. The code word itself defines an interval of real numbers between 0 and 1. As the number of symbols in the message increases, the interval used to represent it becomes smaller and the number of information units (say, bits) required to represent the interval becomes larger. Each symbol of the message reduces the size of the interval in accordance with its probability of occurrence. Because the technique does not require, as does Huffman's approach, that each source symbol translate into an integral number of code symbols (that is, that the symbols be coded one at a time), it achieves (but only in theory) the bound established by the noiseless coding theorem.
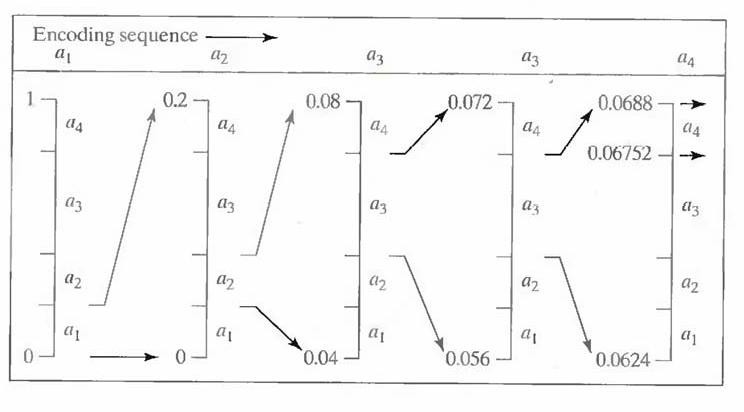
Fig.5.1 Arithmetic coding procedure
Figure 5.1 illustrates the basic arithmetic coding process. Here, a five-symbol sequence or message, a1a2a3a3a4, from a four-symbol source is coded. At the start of the coding process, the message is assumed to occupy the entire half-open interval [0, 1). As Table 5.2 shows, this interval is initially subdivided into four regions based on the probabilities of each source symbol. Symbol ax, for example, is associated with subinterval [0, 0.2). Because it is the first symbol of the message being coded, the message interval is initially narrowed to [0, 0.2). Thus in Fig. 5.1 [0, 0.2) is expanded to the full height of the figure and its end points labeled by the values of the narrowed range. The narrowed range is then subdivided in accordance with the original source symbol probabilities and the process continues with the next message symbol.

Table 5.1 Arithmetic coding example
In this manner, symbol a2 narrows the subinterval to [0.04, 0.08), a3 further narrows it to [0.056, 0.072), and so on. The final message symbol, which must be reserved as a special end-of-message indicator, narrows the range to [0.06752, 0.0688). Of course, any number within this subinterval—for example, 0.068—can be used to represent the message.
In the arithmetically coded message of Fig. 5.1, three decimal digits are used to represent the five-symbol message. This translates into 3/5 or 0.6 decimal digits per source symbol and compares favorably with the entropy of the source, which is 0.58 decimal digits or 10- ary units/symbol. As the length of the sequence being coded increases, the resulting arithmetic code approaches the bound established by the noiseless coding theorem.
In practice, two factors cause coding performance to fall short of the bound: (1) the addition of the end-of-message indicator that is needed to separate one message from an- other; and (2) the use of finite precision arithmetic. Practical implementations of arithmetic coding address the latter problem by introducing a scaling strategy and a rounding strategy (Langdon and Rissanen [1981]). The scaling strategy renormalizes each subinterval to the [0, 1) range before subdividing it in accordance with the symbol probabilities. The rounding strategy guarantees that the truncations associated with finite precision arithmetic do not prevent the coding subintervals from being represented accurately.