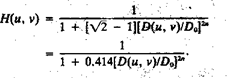Discuss about Butterworth lowpass filter with a suitable example.
Butterworth filter:
The transfer function of the Butterworth lowpass (BLPF) of order n and with cutoff frequency locus at a distance Do, from the origin is defined by the relation
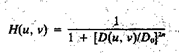
A perspective plot and cross section of the BLPF function are shown in figure 4.
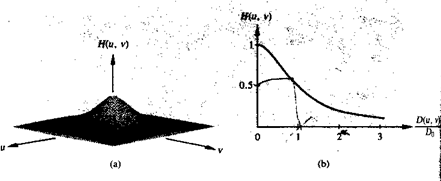
Fig.4 (a) A Butterworth lowpass filter (b) radial cross section for n = 1.
Unlike the ILPF, the BLPF transfer function does not have a sharp discontinuity that establishes a clear cutoff between passed and filtered frequencies. For filters with smooth transfer functions, defining a cutoff frequency locus at points for which H (u, v) is down to a certain fraction of its maximum value is customary. In the case of above Eq. H (u, v) = 0.5 (down 50 percent from its maximum value of 1) when D (u, v) = Do. Another value commonly used is 1/√2 of the maximum value of H (u, v). The following simple modification yields the desired value when D (u, v) = Do: