Explain the concept of homomorphic filtering.
Homomorphic filtering:
The illumination-reflectance model can be used to develop a frequency domain procedure for improving the appearance of an image by simultaneous gray-level range compression and contrast enhancement. An image f(x, y) can be expressed as the product of illumination and reflectance components:
![]()
Equation above cannot be used directly to operate separately on the frequency components of illumination and reflectance because the Fourier transform of the product of two functions is not separable; in other words,
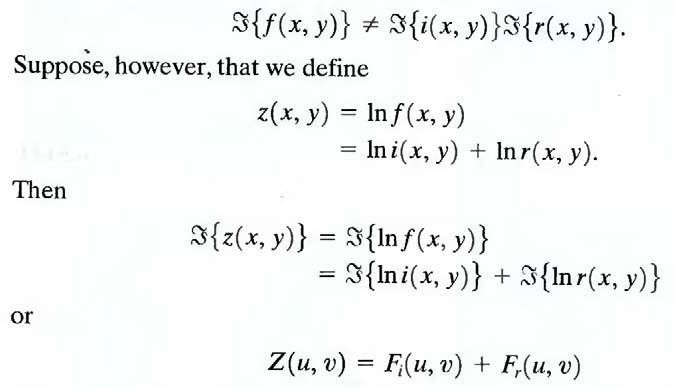
where Fi (u, v) and Fr (u, v) are the Fourier transforms of ln i(x, y) and ln r(x, y), respectively. If we process Z (u, v) by means of a filter function H (u, v) then, from
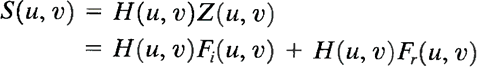
where S (u, v) is the Fourier transform of the result. In the spatial domain,
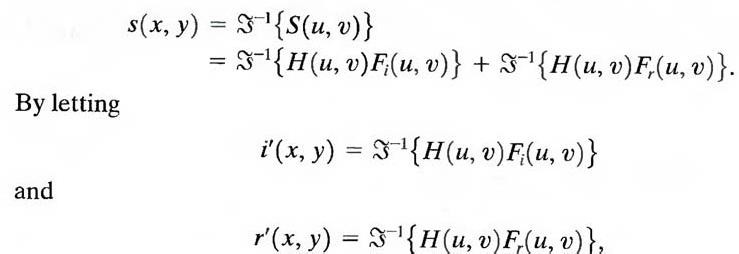
Now we have
![]()
Finally, as z (x, y) was formed by taking the logarithm of the original image f (x, y), the inverse (exponential) operation yields the desired enhanced image, denoted by g(x, y); that is,
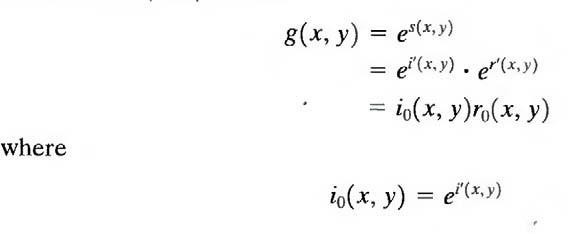

Fig.9.1 Homomorphic filtering approach for image enhancement
and
![]()
are the illumination and reflectance components of the output image. The enhancement approach using the foregoing concepts is summarized in Fig. 9.1. This method is based on a special case of a class of systems known as homomorphic systems. In this particular application, the key to the approach is the separation of the illumination and reflectance components achieved. The homomorphic filter function H (u, v) can then operate on these components separately.
The illumination component of an image generally is characterized by slow spatial variations, while the reflectance component tends to vary abruptly, particularly at the junctions of dissimilar objects. These characteristics lead to associating the low frequencies of the Fourier transform of the logarithm of an image with illumination and the high frequencies with reflectance. Although these associations are rough approximations, they can be used to advantage in image enhancement.
A good deal of control can be gained over the illumination and reflectance components with a homomorphic filter. This control requires specification of a filter function H (u, v) that affects the low- and high-frequency components of the Fourier transform in different ways. Figure 9.2 shows a cross section of such a filter. If the parameters γL and γH are chosen so that γL < 1 and γH > 1, the filter function shown in Fig. 9.2 tends to decrease the contribution made by the low frequencies (illumination) and amplify the contribution made by high frequencies (reflectance). The net result is simultaneous dynamic range compression and contrast enhancement.
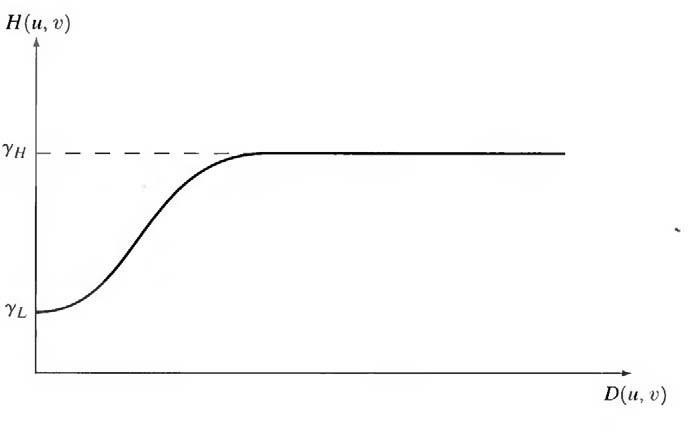
Fig.9.2 Cross section of a circularly symmetric filter function D (u. v) is the distance from the origin of the centered transform.