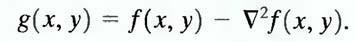Explain how Laplacian is implemented in Frequency Domain
The Laplacian in the Frequency Domain:
It can be shown that

From this simple expression, it follows that
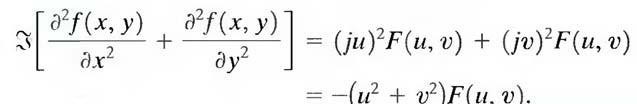
The expression inside the brackets on the left side of the above Eq. is recognized as the Laplacian of f(x, y). Thus, we have the important result

which simply says that the Laplacian can be implemented in the frequency domain by using the filter

As in all filtering operations, the assumption is that the origin of F (u, v) has been centered by performing the operation f(x, y) (-1) x+y prior to taking the transform of the image. If f (and F) are of size M X N, this operation shifts the center transform so that (u, v) = (0, 0) is at point (M/2, N/2) in the frequency rectangle. As before, the center of the filter function also needs to be shifted:
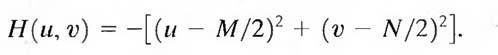
The Laplacian-filtered image in the spatial domain is obtained by computing the inverse Fourier transform of H (u, v) F (u, v):
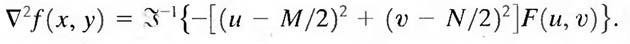
Conversely, computing the Laplacian in the spatial domain and computing the Fourier transform of the result is equivalent to multiplying F(u, v) by H(u, v). We express this dual relationship in the familiar Fourier-transform-pair notation
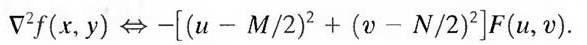
The spatial domain Laplacian filter function obtained by taking the inverse Fourier transform of Eq. has some interesting properties, as Fig.7 shows.
Figure 7(a) is a 3-D perspective plot. The function is centered at (M/2, N/2), and its value at the top of the dome is zero. All other values are negative. Figure 7(b) shows H (u, v) as an image, also centered.
Figure 7(c) is the Laplacian in the spatial domain, obtained by multiplying by H (u, v) by (-1)u+v , taking the inverse Fourier transform, and multiplying the real part of the result by (-l)x+y . Figure 7(d) is a zoomed section at about the origin of Fig.7(c).'
Figure 7(e) is a horizontal gray-level profile passing through the center of the zoomed section. Finally, Fig.7 (f) shows the mask to implement the definition of the discrete Laplacian in the spatial domain.

Fig.7 (a) 3-D plot of Laplacian in the frequency domain, (b) Image representation of (a), (c) Laplacian in the spatial domain obtained from the inverse DFT of (b) (d) Zoomed section of the origin of (c). (e) Gray-level profile through the center of (d). (f) Laplacian mask
A horizontal profile through the center of this mask has the same basic shape as the profile in Fig. 7(e) (that is, a negative value between two smaller positive values). We form an enhanced image g(x, y) by subtracting the Laplacian from the original image: