Write about perspective image transformation.
A perspective transformation (also called an imaging transformation) projects 3D points onto a plane. Perspective transformations play a central role in image processing because they provide an approximation to the manner in which an image is formed by viewing a 3D world. These transformations are fundamentally different, because they are nonlinear in that they involve division by coordinate values.
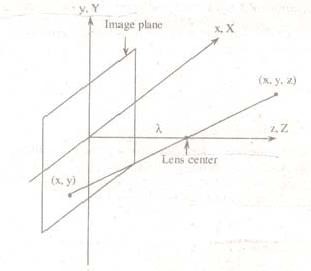
Figure 10 shows a model of the image formation process. The camera coordinate system (x, y, z) has the image plane coincident with the xy plane and the optical axis (established by the center of the lens) along the z axis. Thus the center of the image plane is at the origin, and the centre of the lens is at coordinates (0.0, λ). If the camera is in focus for distant objects, λ is the focal length of the lens. Here the assumption is that the camera coordinate system is aligned with the world coordinate system (X, Y, Z).
Let (X, Y, Z) be the world coordinates of any point in a 3-D scene, as shown in the Fig. 10. We assume throughout the following discussion that Z> λ; that is all points of interest lie in front of the lens. The first step is to obtain a relationship that gives the coordinates (x, y) of the projection of the point (X. Y, Z) onto the image plane. This is easily accomplished by the use of similar triangles. With reference to Fig. 10,