Explain in detail the threshold selection based on boundary characteristics.
Use of Boundary Characteristics for Histogram Improvement and Local Thresholding:
It is intuitively evident that the chances of selecting a "good" threshold are enhanced considerably if the histogram peaks are tall, narrow, symmetric, and separated by deep valleys. One approach for improving the shape of histograms is to consider only those pixels that lie on or near the edges between objects and the background. An immediate and obvious improvement is that histograms would be less dependent on the relative sizes of objects and the background. For instance, the histogram of an image composed of a small object on a large background area (or vice versa) would be dominated by a large peak because of the high concentration of one type of pixels.
If only the pixels on or near the edge between object and the background were used, the resulting histogram would have peaks of approximately the same height. In addition, the probability that any of those given pixels lies on an object would be approximately equal to the probability that it lies on the back-ground, thus improving the symmetry of the histogram peaks.
Finally, as indicated in the following paragraph, using pixels that satisfy some simple measures based on gradient and Laplacian operators has a tendency to deepen the valley between histogram peaks.
The principal problem with the approach just discussed is the implicit assumption that the edges between objects and background arc known. This information clearly is not available during segmentation, as finding a division between objects and background is precisely what segmentation is all about. However, an indication of whether a pixel is on an edge may be obtained by computing its gradient. In addition, use of the Laplacian can yield information regarding whether a given pixel lies on the dark or light side of an edge. The average value of the Laplacian is 0 at the transition of an edge, so in practice the valleys of histograms formed from
the pixels selected by a gradient/Laplacian criterion can be expected to be sparsely populated. This property produces the highly desirable deep valleys.
The gradient Aƒ at any point (x, y) in an image can be found. Similarly, the Laplacian A2f can also be found. These two quantities may be used to form a three-level image, as follows:
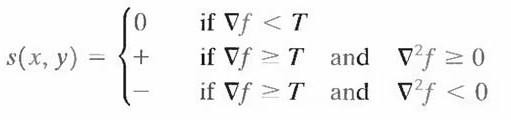
where the symbols 0, +, and - represent any three distinct gray levels, T is a threshold, and the gradient and Laplacian are computed at every point (x, y). For a dark object on a light background, the use of the Eqn. produces an image s(x, y) in which (1) all pixels that are not on
an edge (as determined by Aƒ being less than T) are labeled 0; (2) all pixels on the dark side of an edge are labeled +; and (3) all pixels on the light side of an edge are labeled -. The symbols + and - in Eq. above are reversed for a light object on a dark background. Figure 6.1 shows the
labeling produced by Eq. for an image of a dark, underlined stroke written on a light background.
The information obtained with this procedure can be used to generate a segmented, binary image in which l's correspond to objects of interest and 0's correspond to the background. The transition (along a horizontal or vertical scan line) from a light background to a dark object must be characterized by the occurrence of a - followed by a + in s (x, y). The interior of the object is composed of pixels that are labeled either 0 or +. Finally, the transition from the object back to the background is characterized by the occurrence of a + followed by a -. Thus a horizontal or vertical scan line containing a section of an object has the following structure:
![]()

Fig.6.1 Image of a handwritten stroke coded by using Eq. discussed above
where (…) represents any combination of +, -, and 0. The innermost parentheses contain object points and are labeled 1. All other pixels along the same scan line are labeled 0, with the exception of any other sequence of (- or +) bounded by (-, +) and (+, -).

Fig.6.2 (a) Original image, (b) Image segmented by local thresholding.
Figure 6.2 (a) shows an image of an ordinary scenic bank check. Figure 6.3 shows the histogram as a function of gradient values for pixels with gradients greater than 5. Note that this histogram has two dominant modes that are symmetric, nearly of the same height, and arc separated by a distinct valley. Finally, Fig. 6.2(b) shows the segmented image obtained by with T at or near the midpoint of the valley. Note that this example is an illustration of local thresholding, because the value of T was determined from a histogram of the gradient and Laplacian, which are local properties.
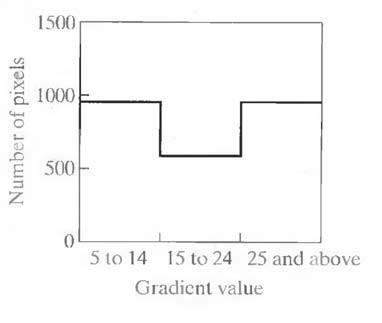
Fig.6.3 Histogram of pixels with gradients greater than 5