What are the derivative operators useful in image segmentation? Explain their role in segmentation.
Gradient operators:
First-order derivatives of a digital image are based on various approximations of the 2-D gradient. The gradient of an image f (x, y) at location (x, y) is defined as the vector
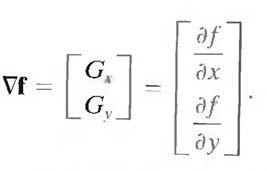
It is well known from vector analysis that the gradient vector points in the direction of maximum rate of change of f at coordinates (x, y). An important quantity in edge detection is the magnitude
of this vector, denoted by Af, where
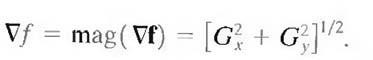
This quantity gives the maximum rate of increase of f (x, y) per unit distance in the direction of Af. It is a common (although not strictly correct) practice to refer to Af also as the gradient. The direction of the gradient vector also is an important quantity. Let α (x, y) represent the direction angle of the vector Af at (x, y). Then, from vector analysis,
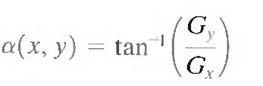
where the angle is measured with respect to the x-axis. The direction of an edge at (x, y) is perpendicular to the direction of the gradient vector at that point. Computation of the gradient of
an image is based on obtaining the partial derivatives &f/&x and &f/&y at every pixel location. Let the 3x3 area shown in Fig. 1.1 (a) represent the gray levels in a neighborhood of an image. One of the simplest ways to implement a first-order partial derivative at point z5 is to use the
following Roberts cross-gradient operators:
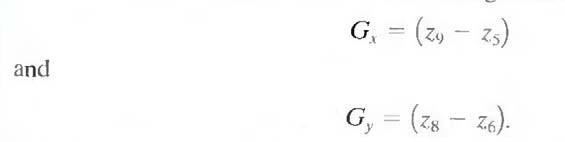
These derivatives can be implemented for an entire image by using the masks shown in Fig. 1.1(b). Masks of size 2 X 2 are awkward to implement because they do not have a clear center. An approach using masks of size 3 X 3 is given by

Fig.1.1 A 3 X 3 region of an image (the z’s are gray-level values) and various masks used to compute the gradient at point labeled z5.
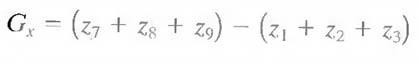
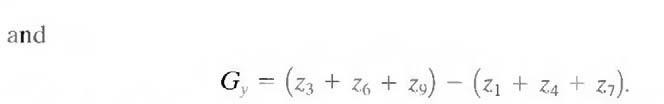
A weight value of 2 is used to achieve some smoothing by giving more importance to the center point. Figures 1.1(f) and (g), called the Sobel operators, and are used to implement these two equations. The Prewitt and Sobel operators are among the most used in practice for computing digital gradients. The Prewitt masks are simpler to implement than the Sobel masks, but the latter have slightly superior noise-suppression characteristics, an important issue when dealing with derivatives. Note that the coefficients in all the masks shown in Fig. 1.1 sum to 0, indicating that they give a response of 0 in areas of constant gray level, as expected of a derivative operator.
The masks just discussed are used to obtain the gradient components Gx and Gy. Computation of the gradient requires that these two components be combined. However, this implementation is not always desirable because of the computational burden required by squares and square roots. An approach used frequently is to approximate the gradient by absolute values:
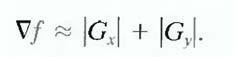
This equation is much more attractive computationally, and it still preserves relative changes in gray levels. However, this is not an issue when masks such as the Prewitt and Sobel masks are used to compute Gx and Gy.
It is possible to modify the 3 X 3 masks in Fig. 1.1 so that they have their strongest responses along the diagonal directions. The two additional Prewitt and Sobel masks for detecting discontinuities in the diagonal directions are shown in Fig. 1.2.
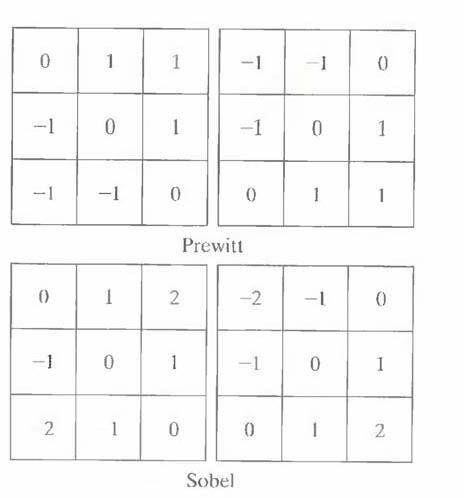
Fig.1.2 Prewitt and Sobel masks for detecting diagonal edges
The Laplacian:
The Laplacian of a 2-D function f(x, y) is a second-order derivative defined as
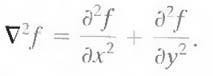
For a 3 X 3 region, one of the two forms encountered most frequently in practice is
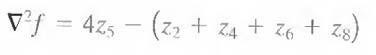
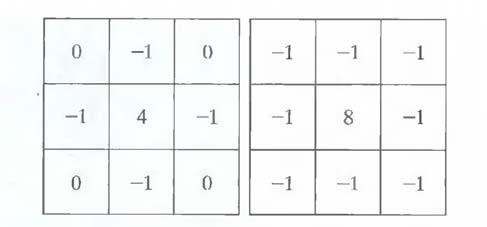
Fig.1.3 Laplacian masks used to implement Eqns. above.
where the z's are defined in Fig. 1.1(a). A digital approximation including the diagonal neighbors is given by
![]()
Masks for implementing these two equations are shown in Fig. 1.3. We note from these masks that the implementations of Eqns. are isotropic for rotation increments of 90° and 45°, respectively.