What is meant by the Gradiant and the Laplacian? Discuss their role in image enhancement.
Use of Second Derivatives for Enhancement–The Laplacian:
The approach basically consists of defining a discrete formulation of the second-order derivative and then constructing a filter mask based on that formulation. We are interested in isotropic filters, whose response is independent of the direction of the discontinuities in the image to which the filter is applied. In other words, isotropic filters are rotation invariant, in the sense that rotating the image and then applying the filter gives the same result as applying the filter to the image first and then rotating the result.
Development of the method:
It can be shown (Rosenfeld and Kak [1982]) that the simplest isotropic derivative operator is the Laplacian, which, for a function (image) f(x, y) of two variables, is defined as
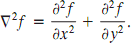
Because derivatives of any order are linear operations, the Laplacian is a linear operator. In order to be useful for digital image processing, this equation needs to be expressed in discrete form. There are several ways to define a digital Laplacian using neighborhoods. digital second.Taking into account that we now have two variables, we use the following notation for the partial second-order derivative in the x-direction:
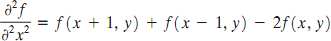
and, similarly in the y-direction, as
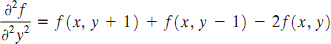
The digital implementation of the two-dimensional Laplacian in Eq. is obtained by summing these two components
![]()
This equation can be implemented using the mask shown in Fig.11.1(a), which gives an isotropic result for rotations in increments of 90°.
The diagonal directions can be incorporated in the definition of the digital Laplacian by adding two more terms to Eq., one for each of the two diagonal directions.The form of each new term is the same as either Eq

Fig.11.1. (a) Filter mask used to implement the digital Laplacian (b) Mask used to implement an extension of this equation that includes the diagonal neighbors. (c) and (d) Two other implementations of the Laplacian.
but the coordinates are along the diagonals. Since each diagonal term also contains a –2f(x, y) term, the total subtracted from the difference terms now would be –8f(x, y). The mask used to implement this new definition is shown in Fig.11.1(b). This mask yields isotropic results for increments of 45°. The other two masks shown in Fig. 11 also are used frequently in practice.
They are based on a definition of the Laplacian that is the negative of the one we used here. As such, they yield equivalent results, but the difference in sign must be kept in mind when combining (by addition or subtraction) a Laplacian-filtered image with another image.
Because the Laplacian is a derivative operator, its use highlights gray-level discontinuities in an image and deemphasizes regions with slowly varying gray levels.This will tend to produce images that have grayish edge lines and other discontinuities, all superimposed on a dark, featureless background.Background features can be ―recovered‖ while still preserving the sharpening effect of the Laplacian operation simply by adding the original and Laplacian images. As noted in the previous paragraph, it is important to keep in mind which definition of the Laplacian is used. If the definition used has a negative center coefficient, then we subtract, rather
than add, the Laplacian image to obtain a sharpened result.Thus, the basic way in which we use the Laplacian for image enhancement is as follows:
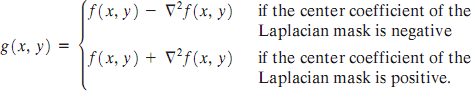
Use of First Derivatives for Enhancement—The Gradient:
First derivatives in image processing are implemented using the magnitude of the gradient. For a function f(x, y), the gradient of f at coordinates (x, y) is defined as the two-dimensional column vector
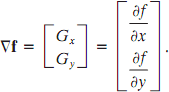
The magnitude of this vector is given by
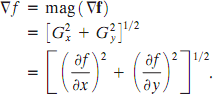
The components of the gradient vector itself are linear operators, but the magnitude of this vector obviously is not because of the squaring and square root operations. On the other hand, the partial derivatives are not rotation invariant (isotropic), but the magnitude of the gradient vector is. Although it is not strictly correct, the magnitude of the gradient vector often is referred to as the gradient.
The computational burden of implementing over an entire image is not trivial, and it is common practice to approximate the magnitude of the gradient by using absolute values instead of squares and square roots:
![]()
This equation is simpler to compute and it still preserves relative changes in gray levels, but the isotropic feature property is lost in general. However, as in the case of the Laplacian, the isotropic properties of the digital gradient defined in the following paragraph are preserved only for a limited number of rotational increments that depend on the masks used to approximate the derivatives. As it turns out, the most popular masks used to approximate the gradient give the same result only for vertical and horizontal edges and thus the isotropic properties of the gradient are preserved only for multiples of 90°.
As in the case of the Laplacian, we now define digital approximations to the preceding equations, and from there formulate the appropriate filter masks. In order to simplify the discussion that follows, we will use the notation in Fig. 11.2 (a) to denote image points in a 3 x 3 region. For example, the center point, z5 , denotes f(x, y), z1 denotes f(x- 1, y-1), and so on. The simplest approximations to a first-order derivative that satisfy the conditions stated in that section are Gx = (z8 –z5) and Gy = (z6 – z5) . Two other definitions proposed by Roberts [1965] in the early development of digital image processing use cross differences:
![]()
we compute the gradient as
![]()
If we use absolute values, then substituting the quantities in the equations gives us the following approximation to the gradient:
![]()
If we use absolute values, then substituting the quantities in the equations gives us the following approximation to the gradient:
![]()
This equation can be implemented with the two masks shown in Figs. 11.2 (b) and(c). These masks are referred to as the Roberts cross-gradient operators. Masks of even size are awkward to implement. The smallest filter mask in which we are interested is of size 3 x 3.An approximation using absolute values, still at point z5 , but using a 3*3 mask, is
![]()
The difference between the third and first rows of the 3 x 3 image region approximates the derivative in the x-direction, and the difference between the third and first columns approximates the derivative in the y-direction. The masks shown in Figs. 11.2 (d) and (e), called the Sobel operators. The idea behind using a weight value of 2 is to achieve some smoothing by giving more importance to the center point. Note that the coefficients in all the masks shown in Fig.
11.2 sum to 0, indicating that they would give a response of 0 in an area of constant gray level, as expected of a derivative operator.
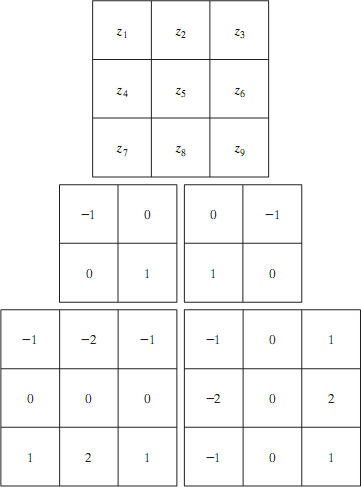
Fig.11.2 A 3 x 3 region of an image (the z’s are gray-level values) and masks used to compute the gradient at point labeled z5 . All masks coefficients sum to zero, as expected of a derivative operator.